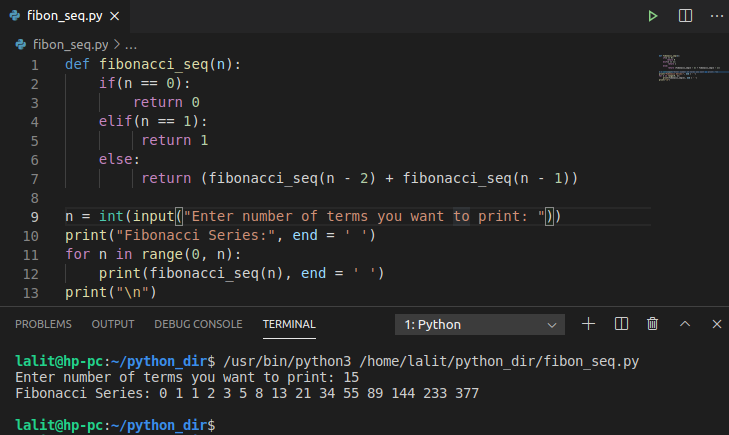
How do you write a Fibonacci Series in Python?

The Fibonacci Series is an important daily life concept which also mandatorily comes in school syllabuses. Thanks to its founder, Leonardo Fibonacci, the series concept has made a huge significance in the data structure and algorithm world.

Do you know this concept was well-known to Indian mathematicians in the 6th century itself? Yes! Alright, facts apart, what is the Fibonacci Sequence?

The Fibonacci Series is an arrangement of numbers which are all determined by adding the initial numbers followed by adding the previous two values.

For eg: if the first two numbers are 8 and 9, the third number will be the total of 8 and 9 that is 17. Then, to get the fourth number, we add 9 and 17 which is 26. So the series will look like 8, 9, 17, 26 and so on.

Now, the Fibonacci Series has been long used in the world of code and it has invented massive software. In this article, we will particularly look at how the Python Fibonacci Series can be printed with relevant examples.

Methods to Code FibonacciSeries in Python

Speaking of the methods in which a Fibonacci sequence can be printed, there are primarily two types. Let us briefly look into them for better understanding.

Recursive Method

Fibonacci problems are usually explored using recursion methods. Recursion is defined as the process through which a function calls itself so that it can break down a problem so the solution can be found easily. Until the base case is reached, recursion will keep calling itself to keep breaking the problem.

Once it reaches the base case, it will send out the result to whichever immediate function called it and finally the result will be sent to the first function which originally started the recursion.

To get the required Fibonacci pattern, the recursive code will keep calling itself until the result comes. For example, firstly the user must tick off the base case in fibonacci_of(). Then if the ‘n’ is 15, that is you want 15 Fibonaccinumbers then you keep calling the function until all the preceding two numbers get added for the next number.

If the size of ‘n’ increases, the process also takes long but usually when the size is around 50, it can crash and cause subproblems due to hardware problems. Recursion also uses the memoization technique which will further see below.

What is Memoization?

As we saw, recursion calls itself until the result is out but what if we tell you can save the time by storing that process? Yes, in a memory cache like Python list, we can store the previously made function calls so when we want to do another Fibonacci sequence, it will start all over again. This time-consuming method is called Memoization.

Memoization not only saves time but also fastens the program to give results quickly. It will not have to repeat the whole process, rather will help the code to quickly garner information without having to heat the hardware as well.

Iteration Method

If you’re not a fan of recursively calling a function, then the iterative method can be employed which will find the value of the desired ‘n’. We already know that if the first two values are, say, 8 and 9, then the third will be 17, as the previous numbers get added for the next value. Thus, iteratively you can create a loop which will on its own do this adding function. That is, we first store the initial inputs that are 8 and 9 in cache. Next, we will compute the further numbers in a loop until it terminates.

As we already manually printed the first two numbers, you should reduce from the totally needed numbers. That is, if you want 15 Fibonacci numbers, type the value of n as 13, because already two numbers are printed. Then start the iterative loop from the 3rd value, so it will continue to print until the last value of the series is found.

Note: Iterative and Recursion methods are two popular methods which not only works with Python, but also helps in printing Fibonacci series program in C++ and Java.

How does time and space complexity work?

Time complexity is nothing but the technique through which the total time took by an algorithm to finish is calculated. It takes note of every code’s execution time. When we speak of the recursion method, the time complexity will be O(n) as it keeps calling the functions until the required numbers are printed. Similarly O(n) is the time complexity of the iteration method as well as it keeps looping until the desired result is out.

On the other hand, space complexity is just the technique to measure how much space the algorithm took while executing a code. In the recursion method, as it uses a call stack, O(n) is the space complexity. Call stack is the memory stack that stores all the data to be used for future purposes. In terms of the iteration method, due to not taking additional space the space complexity will be O(1).

Final Thoughts

Learning how to print Fibonacci series in Python will help you to deepen your programming knowledge as it explores one of the popular methods of “recursion.” Additionally, you will also learn how codes iteratively work to reach the limit.

If you’re preparing for a coding interview, learning about Python and Fibonacci sequence will definitely help you. We wish you all the best for your coding journey.